CVP analysis relies on all of the following assumptions except for one crucial exception. This assumption, which is often overlooked, can have a significant impact on the accuracy and reliability of CVP analysis results.

In this article, we will explore this exceptional assumption, examining its limitations and implications for CVP analysis. We will also discuss strategies for addressing this assumption when it is not met.

Assumption of Normality

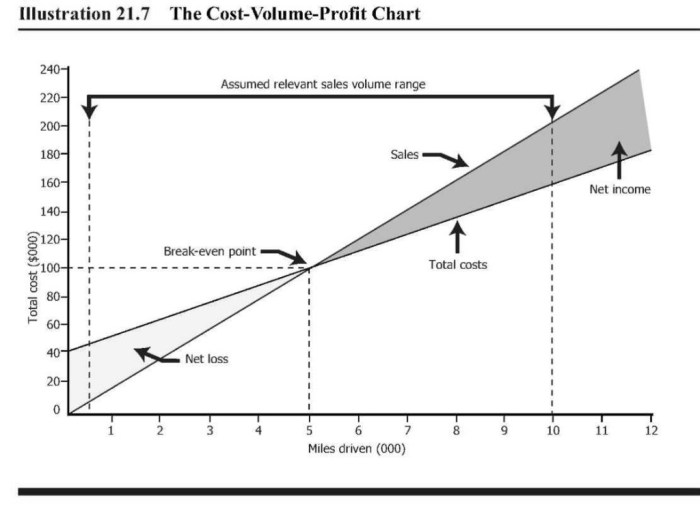
CVP analysis assumes that the distribution of activity levels is normal. This assumption is important because it allows for the use of statistical techniques, such as regression analysis, to estimate the relationship between costs and volume. However, there are a number of situations in which the assumption of normality may be violated.

Examples of When the Assumption of Normality is Violated

• When the activity level is skewed, meaning that there are more observations at one end of the distribution than the other.
• When the activity level is bimodal, meaning that there are two peaks in the distribution.
• When the activity level is multimodal, meaning that there are more than two peaks in the distribution.

The impact of violating the assumption of normality on CVP analysis can be significant. If the assumption is violated, then the regression analysis may not be able to accurately estimate the relationship between costs and volume. This can lead to inaccurate predictions of costs and profits.

Methods to Address Non-Normality in CVP Analysis

• Transform the data so that it is more normally distributed.
• Use a non-parametric statistical technique, such as the Kruskal-Wallis test.
• Use a bootstrapping technique to estimate the relationship between costs and volume.

Assumption of Linearity

CVP analysis assumes that the relationship between costs and volume is linear. This assumption is important because it allows for the use of simple mathematical equations to estimate the impact of changes in volume on costs. However, there are a number of situations in which the assumption of linearity may not be realistic.

Limitations of Assuming Linearity in CVP Analysis

• The relationship between costs and volume may be curvilinear, meaning that it may not be a straight line.
• The relationship between costs and volume may be stepped, meaning that there may be sudden changes in costs at certain levels of volume.

The consequences of non-linear relationships between costs and volume can be significant. If the assumption of linearity is violated, then the CVP analysis may not be able to accurately predict the impact of changes in volume on costs. This can lead to inaccurate predictions of profits.

Examples of Non-Linear Cost Functions, Cvp analysis relies on all of the following assumptions except

• A cost function that is curvilinear may have a U-shape, meaning that costs increase at a decreasing rate as volume increases.
• A cost function that is stepped may have a step-wise shape, meaning that costs increase suddenly at certain levels of volume.

Assumption of Single Cost Driver

CVP analysis assumes that there is a single cost driver that explains the relationship between costs and volume. This assumption is important because it allows for the use of simple mathematical equations to estimate the impact of changes in volume on costs.

However, there are a number of situations in which the assumption of a single cost driver may not be realistic.

Why the Assumption of a Single Cost Driver May Not Be Realistic

• There may be multiple cost drivers that affect the relationship between costs and volume.
• The relationship between costs and volume may be non-linear, meaning that it may not be a straight line.

The challenges of identifying and using multiple cost drivers can be significant. If there are multiple cost drivers, then it may be difficult to determine which cost driver is the most important. Additionally, it may be difficult to develop a mathematical equation that accurately predicts the impact of changes in volume on costs.

Examples of Situations Where Multiple Cost Drivers Are Present

• A manufacturing company may have multiple cost drivers, such as labor costs, material costs, and overhead costs.
• A retail company may have multiple cost drivers, such as sales volume, customer traffic, and the number of employees.

Assumption of Constant Cost Behavior

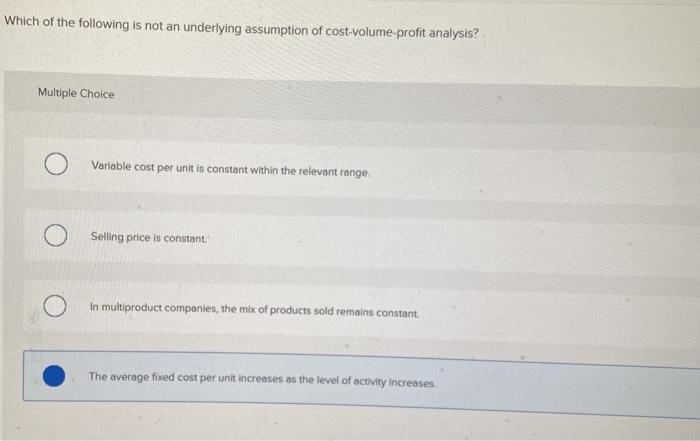
CVP analysis assumes that costs are constant within the relevant range of activity. This assumption is important because it allows for the use of simple mathematical equations to estimate the impact of changes in volume on costs. However, there are a number of situations in which the assumption of constant cost behavior may not be realistic.

Types of Costs That Do Not Exhibit Constant Behavior

• Variable costs are costs that change in proportion to changes in volume.
• Fixed costs are costs that do not change in proportion to changes in volume.
• Semi-variable costs are costs that have both variable and fixed components.

The implications of non-constant cost behavior for CVP analysis can be significant. If the assumption of constant cost behavior is violated, then the CVP analysis may not be able to accurately predict the impact of changes in volume on costs.

This can lead to inaccurate predictions of profits.

Methods to Account for Non-Constant Cost Behavior

• Use a more sophisticated cost accounting system, such as activity-based costing (ABC).
• Use a non-linear cost function to estimate the impact of changes in volume on costs.

Assumption of Relevant Range

CVP analysis assumes that the data used to develop the CVP model is within the relevant range of activity. The relevant range is the range of activity levels over which the assumptions of the CVP model are valid. If the data used to develop the CVP model is outside the relevant range, then the CVP model may not be able to accurately predict the impact of changes in volume on costs.

Define the Relevant Range and Explain Its Importance in CVP Analysis

The relevant range is the range of activity levels over which the assumptions of the CVP model are valid. The relevant range is important because it ensures that the CVP model is only used to make predictions about activity levels that are within the range of activity levels for which the model was developed.

Consequences of Using Data Outside the Relevant Range

• The CVP model may not be able to accurately predict the impact of changes in volume on costs.
• The CVP model may overestimate or underestimate costs.
• The CVP model may lead to inaccurate predictions of profits.

Examples of How to Determine the Relevant Range

• Use historical data to determine the range of activity levels that have occurred in the past.
• Use industry data to determine the range of activity levels that are typical for similar businesses.
• Use a sensitivity analysis to determine the impact of changes in activity levels on costs.

FAQ Resource: Cvp Analysis Relies On All Of The Following Assumptions Except

What is the exceptional assumption in CVP analysis?

The exceptional assumption in CVP analysis is that costs behave in a constant and linear manner.

What are the implications of violating the exceptional assumption?

Violating the exceptional assumption can lead to inaccurate and unreliable CVP analysis results.

How can practitioners address the exceptional assumption when it is not met?

Practitioners can address the exceptional assumption by using more sophisticated cost estimation techniques, such as activity-based costing.